Los juegos de azar y la falacia de los jugadores
Insólito en Montecarlo : La bolita fue al "negro" por 26 veces consecutivas.
La falacia del jugador, también conocida como la falacia de Monte Carlo toma ese nombre en función al famoso casino que es uno de los atractivos turísticos más notables del Principado de Mónaco.

El complejo del casino es un sistema de juegos de azar que incluye también el Gran Teatro de Montecarlo, una ópera y una casa de ballet, y la sede de los Ballets de Montecarlo. Está situado en el distrito de Montecarlo, aunque para los ciudadanos de Mónaco está prohibido entrar en las salas de juego. Era la sede anual de la Gran Final del Tour europeo de Pokér (European Poker Tour Grand Final), siendo sustituido por el Gran Casino de Madrid.
El casino es propiedad de la Société des Bains de Mer (Euronext: MC0000031187), una empresa pública, en la que el gobierno tiene una participación mayoritaria. Esta empresa también es propietaria de los principales hoteles y clubes de la comunidad que sirven a la industria turística monegasca.
El caso es que la falacia alude a la errónea creencia de que si algo sucede de una manera más frecuente de lo normal durante un periodo de tiempo, entonces sucederá con menor frecuencia en el futuro; es decir esa conceptualización de lo que muchos entienden qué es la probabilidad observada varias veces en sus sucesos. Vale decir , si algo sucede de una manera menos frecuente de lo normal durante un periodo de tiempo, entonces sucederá con más frecuencia en el futuro (presumiblemente por un instinto de equilibrio natural). En situaciones en que se observa algo poco habitual , en rigor entonces los entendidos advierten que esta creencia de que se gana según la frecuencia de los resultados, aunque atractiva para la mente humana, es falsa.
Esta falacia se puede dar en muchas situaciones prácticas aunque está más asociada con el juego, donde tales errores son comunes entre jugadores.

La falacia del jugador es la errónea creencia de que un proceso aleatorio se vuelve menos aleatorio y más predecible a medida que se repite. Por ejemplo, una persona jugando a tirar los dados puede sentir que los dados van a sacar un determinado número, basándose en su fracaso de aciertos después de múltiples tiradas.
Esta es una falsa creencia, ya que la posibilidad de que los dados saquen un número es la misma en cada tirada, independientemente de las tiradas anteriores o posteriores. Y eso, ojo, hay que tenerlo meridianamente claro, para no caer en la falacia del jugador, se advierte.
¿CÓMO SUCEDE ESTE ENFOQUE MATEMÁTICO ERRÓNEO?
La falacia del jugador se produce cuando una persona asume que la desviación de lo que ocurra por término medio o a largo plazo será corregido a corto plazo. La falacia sucede de la siguiente manera; según uno puede encontrar esto en textos o en documentos:
X ha sucedido.
X se desvía de lo se espera que ocurra en promedio o a largo plazo.
Por lo tanto, X finalizará pronto.
La persona asume que el resultado será “adecuado” simplemente porque lo que ha pasado previamente se desvía de lo esperado, ya sea en promedio o a largo plazo.

Por ejemplo, el lanzamiento de una moneda (dos caras, no trucada) no afectará al siguiente lanzamiento de esa moneda. Así que cada vez que se lanza la moneda habrá un 50% de posibilidades que salga cara y un 50% de posibilidades que salga cruz. Supongamos que una persona lanza una moneda 6 veces y sale cara cada una de las veces.
Si saca la conclusión de que la próxima vez que tire la moneda saldrá cruz, porque “toca”, entonces habrá cometido la falacia del jugador.
Esto es porque los resultados de los lanzamientos anteriores no tienen efecto sobre el resultado del 7º lanzamiento. Hay 50% de posibilidades que salga cara y 50% que salga cruz, como en cualquier otro lanzamiento la 7ma vez que tire la moneda. Ese fifty fifty no tiene memoria, como muchos erróneamente piensan y ello es muy común.
LA FALACIA DEL JUGADOR SE ORIGINÓ EN LA RULETA DE MONTE CARLO

Por ello uno encuentra esto colgado en el internet: es decir el ejemplo más conocido de este fenómeno ocurrió en un juego de ruleta en el Casino de Monte Carlo el 18 de agosto de 1913, cuando la bola cayó en negro 26 veces seguidas.
Esto es extremadamente insólito, aunque ni más ni menos insólito que cualquiera de las otras 67,108,863 secuencias del 26 rojo o negro. Los jugadores perdieron millones de francos apostando contra el negro, razonando de manera equivocada que la racha estaba causando un “desequilibrio” en el carácter aleatorio de la rueda, y que lo siguiente sería una larga racha de rojos.
Y eso es bien fácil de entender si uno se guía por el sentido común ¿No es cierto?
El tema es entonces campo de la psicología. La falacia del jugador proviene de la creencia en la "ley de números pequeños", o el pensamiento equivocado de que muestreos pequeños deben ser representativos del groso de la población. De acuerdo a la falacia, las “rachas” deben equilibrarse para ser representativas.
La sabiduría popular de expertos en juego y matemáticos nos dice que cada decisión de una mesa de juego (en juegos como la ruleta o dados) es una situación independiente. El argumento contrario (que un número se puede acertar) se considera un punto de vista simplón, y se relaciona con las premisas de la falacia del jugador.
Por lo que parece, esta llamada falacia es falsa. A continuación muestro unos apuntes que pululan en el internet y que vale la pena ponerles la atención debida.
EN LA RULETA AMERICANA, POR EJEMPLO:
• Los expertos están de acuerdo en que cada número tiene 1 posibilidad de 38 de aparecer en la siguiente tirada.
• Esta posibilidad de 1 de 38 se conoce como expectativa estadística de los números.
• Si un ente tiene o toma algún tipo de expectativa deja de ser independiente.
Si estas situaciones numéricas no tuvieran una previsibilidad inherente, no habría manera de asignarles una expectativa estadística. Y cualquier cosa que cuente con una cualidad predecible, no puede ser “independiente”. Tal como Frank Barstow dijo en su libro Gana al Casino en que dice con toda claridad :
"Los dados y la ruleta son impredecibles, pero si su comportamiento no estuviera sujeto a ningún principio ni fuerza que los gobierne, las secuencias de 30 o más repeticiones serían comunes, y no podría haber juegos como la ruleta o craps, porque no habría manera de calcular las probabilidades."
Esto por supuesto va en contra de las creencias y enseñanzas de otros autores del juego, pero eso, en sí mismo, no prueba que la afirmación sea equivocada.
La verdad se hace más clara cuando uno considera que la premisa de “situaciones independientes” que sostienen los expertos en juego se contradice a sí misma. Los resultados de la mesa están en un continuo estado de correspondencia con sus probabilidades, pero cualquier cosa sea realmente “independiente” no se corresponde con nada. Muchos autores de juego se contradicen a sí mismos también, aconsejando a sus lectores mantener una condición específica de mesa .
Si los resultados de la mesa fueran tan independientes como dicen, no habría ningún tipo de influencia cuando un jugador hace sus apuestas. Cualquier cosa que ocurriera en el pasado no tendría ninguna relevancia en absoluto.
Los autores expertos en juego, estadísticos y matemáticos todos afirman que los números se corresponden con las probabilidades siempre y cuando se dé un muestreo suficientemente amplio. Lo que dicen es que los números se corresponden en grupos grandes, pero no en grupos pequeños. Otra contradicción.

Pensemos en la predisposición estadística como una constante subyacente, que será a menudo interrumpida por patrones, ¡que no aceptan órdenes de nadie.
Todos esos expertos, durante todos estos años, han estado equivocados. Es la explicación del 3qA lo que explica esta nueva realidad. Esta es la realidad verdadera. Esta es la explicación que no haría que la comunidad científica se echara a temblar al intentar explicar por qué los números hacen lo que hacen.
Por ello el creer que porque una moneda haya caído 10 veces en cara, a la siguiente ocasión lo hará en cruz porque tiene más probabilidades no es cierto.
Cuando se habla de la Falacia del Apostador, se dice que contiene los siguientes errores y puede ser claramente aplicable a la ruleta:
Un suceso aleatorio tendrá más probabilidades de suceder si no ha ocurrido en un lapso .
Un suceso aleatorio tendrá menos probabilidades de suceder si ha ocurrido en un cierto período.
Si hablamos de la ruleta, la probabilidad de que salga rojo después de que haya salido rojo es la misma que de que salga negro. Es decir, las probabilidades no se irán sumando, sino que será siempre del 50%. Esto contrasta con la Teoría del Caos que nos dice que unos números salen más que otros, aunque dicha teoría, obviamente, es visto en un gran lapso .
¿POR QUÉ SE LLAMA FALACIA DE MONTECARLO?
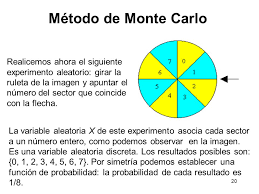
Ojo no confundir con el "Método de Montecarlo" que es una técnica numérica para calcular probabilidades y otras cantidades relacionadas, utilizando secuencias de números aleatorios y que rebasa a lo que estamos mostrando en este post.
Aunque ya lo hemos expuesto lo de la falacia , redundemos:
Los jugadores que estaban sentados entonces en la mesa y veían como caía recurrentemente la bolita en el mismo color, miraban atónitos que la misma iba cayendo una y otra vez en el negro. A partir de la tirada 10, todos los jugadores ya no dudaban en apostar miles de francos al rojo, confiando en que la bola ya tenía que cambiar de color. Pero no. 15, 17, 20, 22 veces seguidas negro…. La gente estaba ya escandalizada y pasaba a apostar millones de francos al rojo, pero la bola seguía cayendo en negro.
No contaban con que la ruleta no tiene memoria. Es decir, porque haya salido anteriormente negro no quiere decir que la próxima vez tenga más posibilidades de salir rojo. Lo confunden con la poca probabilidad de que salga 26 veces seguidas negro. En este caso, cada evento es separado.
De hecho, se calcula que si alguien hubiera puesto un franco al negro en la primera tirada y hubiera continuado apostando por el negro sus ganancias durante toda la secuencia hubiera ganado 67.108.864 francos.
Años más tarde, se creó una teoría matemática llamada Falacia de Montecarlo o Gambler’s Fallacy a raíz de los sucedido esa noche en el casino de Montecarlo.
Sin duda, nos puede servir de aprendizaje para cuando juguemos a la ruleta o a cualquier juego en el que las probabilidades sean similares.
¿Interesante no?
Y además insólito que una bolita haya caído por 26 veces seguidas ese 18 de agosto del año 1913, en pleno desarrollo de la Primera Gran Guerra.
Debe quedar entonces claro, que el mensaje que se discute ampliamente en las escuelas de negocios es que tanta gente que ha perdido dinero en las casas de juego, se debe por no tener claro el tema estadístico.
Y es que sencillamente, las probabilidades de que algo suceda la próxima vez no están necesariamente relacionadas con lo que ya sucedió, especialmente en muchos juegos de azar.
Por ello y valiéndome de lo que ya ha sido escrito tantas veces, señalo que esto suele resumirse en la frase "Los dados (o moneda) no tiene memoria", pues su naturaleza es la misma, independiente del número de tiros y resultados previos.

Para seguir aclarando y redundando en un tema que es simple, pero cuesta razonarlo y aceptarlo, la falacia del jugador puede ilustrarse considerando el lanzamiento repetido de una moneda.
Si ésta está equilibrada, las opciones de que salga cara son exactamente 0,5 (una de cada dos). Las opciones de que salgan dos caras seguidas es 0,5×0,5=0,25 (una de cada cuatro), las de obtener tres caras seguidas son 0,5×0,5×0,5=0,125 (una de cada ocho), y así sucesivamente.
Supongamos que se han sacado cuatro caras seguidas. Un creyente en la falacia del jugador diría: «Si en el siguiente lanzamiento saliese cara, habrían salido cinco consecutivas. La probabilidad de que esto suceda es , así que por tanto en el siguiente lanzamiento la probabilidad de que salga cara es sólo 1 entre 32.»
Éste es el paso falaz en el razonamiento. Si la moneda está equilibrada y se excluye la posibilidad de caer de canto, entonces por definición la probabilidad debe ser siempre 0,5 tanto para cara como para cruz.
Aunque la probabilidad de lograr una serie de cinco caras consecutivas es de sólo 1 cada 32 (0,03125), lo es antes de que la moneda se tire por primera vez. Después de los primeros cuatro lanzamientos los resultados ya no son desconocidos, y por tanto no cuentan.
La probabilidad de lograr cinco caras consecutivas es la misma que la de cuatro caras seguidas de una cruz.
Las cruces no son más probables. Cada uno de los dos posibles resultados tiene la misma probabilidad independientemente del número de veces que la moneda se haya lanzado antes y de los resultados obtenidos.
Razonar que es más probable que el próximo lanzamiento será cruz en vez de cara debido a los anteriores lanzamientos es la falacia: la idea de que una racha de suerte pasada influye de alguna forma en las posibilidades futuras.
A veces los jugadores arguyen: «Acabo de perder cuatro veces seguidas. Como la moneda está equilibrada y por tanto a la larga los resultados lo estarán también, si me limito a seguir jugando terminaré por recuperar mi dinero».
Sin embargo, es irracional considerar las cosas «a la larga» comenzando desde antes de empezar a jugar: debe considerarse a la larga desde la posición actual, y no puede esperarse que el juego se equilibre desde la posición inicial, pues ya se acumulan cuatro juegos perdidos.
Como ejemplo, la estrategia popular de doblar la apuesta (comenzar con 1, si se pierde apostar 2, luego 4, etcétera hasta que se gane) no funciona.

Situaciones como estas se investigan en la teoría matemática de los caminos aleatorios. Esta y otras estrategias parecidas canjean muchas pequeñas ganancias por unas pocas pérdidas enormes (como en este caso) o viceversa.
Con una cantidad infinita de capital disponible, podría adoptarse esta estrategia; en otro caso es mejor apostar una cantidad fija sólo porque es más fácil estimar cuánto puede perderse en una hora o día de juego.

Adviértase que la falacia del jugador es bastante diferente del siguiente hilo de razonamiento (que lleva a la conclusión opuesta): «la moneda da cara más veces que cruz, por lo que no está equilibrada, así que apostaré que en el siguiente lanzamiento también saldrá cara».
Esto no es una falacia, si bien el primer paso (del argumento a partir de un número finito de observaciones a la afirmación de sesgo de la moneda) es muy delicado y en sí mismo proclive a falacias de su propio tipo peculiar.
Un chiste de matemáticos demuestra la naturaleza de la falacia. Cuando vuela en avión, un hombre decide llevar siempre una bomba consigo. «Las probabilidades de que en un avión haya una bomba son muy pequeñas —razona—, ¡así que las probabilidades de que haya dos son casi nulas!»
Algunos afirman que la falacia del jugador es un sesgo cognitivo provocado por una heurística psicológica llamada heurística de la representatividad.
La probabilidad de que una pareja con dos hijas tenga otra es la misma que la de que tenga un hijo, o que la de otra pareja con dos hijos (excluyendo influencias genéticas).
La probabilidad de ganar en la lotería jugando siempre el mismo número es la misma que jugando un número diferente cada vez: las probabilidades sólo dependen de los números en juego.
Así que mi único interés, es haberles mostrado que a veces lo que consideramos, normal, cierto, esconde cosas que a simple vista no vemos.
Y eso sucede mucho en el campo de la economía , con el tema del PBI en que se nos machaca, mañana, tarde y noche que sólo un PBI in crescendo nos saca de perdedores y reduce el problema de los pobres.




